Incorporating uncertainty in portfolio construction

Building resilient, investor-specific portfolios requires a shift away from point estimates for returns. That is why we explicitly include uncertainty into our return projections and can create optimal portfolios by considering multiple return pathways.

Overview Return pathways From theory to practice

Paragraph-2

Paragraph-3

Paragraph-4

Overview

The incorporation of uncertainty is an important part of our revamped approach to portfolio construction. By incorporating uncertainty, we recognize that mean expected returns for assets are estimated with error rather than assuming they are known, as is the case with mean variance techniques. We consider the distribution around the mean, effectively reducing the weight placed on our mean (central) estimate. How much uncertainty should we consider? We highlight some criteria used to identify a suitable amount of uncertainty in our process. They include the back-tested predictive power of our asset class return models, the historic volatility of assets and the desire for diverse portfolios when optimizing. Uncertainty in mean returns feeds into our stochastic simulations, that give a range of potential return pathways from five years out to the long term. When constructing portfolios, these simulated pathways and our mean return uncertainty enable us to use robust optimization techniques that generally lead to less concentrated portfolios compared with those portfolios resulting from mean variance optimization. It also gives flexibility to focus on certain upside or downside scenarios when constructing portfolios to fit client needs.

This information is not intended as a recommendation to invest in any particular asset class or strategy or as a promise -or even estimate -of future performance. Source: BlackRock Investment Institute, April 2019. Data as of 28 February, 2019. Notes: Return assumptions are total nominal returns. US dollar return expectations for all asset classes are shown in unhedged terms, with the exception of global ex-US Treasuries, hedge funds, and global ex-US large cap equities. Our CMAs generate market, or beta, geometric return expectations. Asset return expectations are gross of fees. For a list of indices used, visit our Capital Market Assumptions website at blackrock.com/institutions/en-us/insights/portfolio-design/capital-market-assumptions and click on the information icon in the Asset class return and volatility expectations table. We use BlackRock proxies for selected private markets because of lack of sufficient data. These proxies represent the mix of risk factor exposures that we believe represents the economic sensitivity of the given asset class. There are two sets of bands around our mean return expectation. The darker bands show our estimates of uncertainty in our mean return estimates. The lighter bands are based on the 25th and 75th percentile of expected return outcomes –the interquartile range -of potential return pathways (Garlappi, Wang and Uppal, 2006 ). Indices are unmanaged and used for illustrative purposes only. They are not intended to be indicative of any fund or strategy’s performance. It is not possible to invest directly in an index.

Distinguishing between uncertainty and risk is important. We define uncertainty as the range of outcomes for the mean and risk as the range of outcomes around the mean. For example, instead of saying an asset has a mean return of 6%, we say a mean return in range of 5-7% even if the risk, or volatility, of the asset stays the same. We believe overlooking uncertainty, combined with common mean variance optimization (MVO) techniques, can lead to undesirable results such as unstable or overly concentrated asset allocations without the use of ad-hoc constraints.

Our approach does two important things: First, it acknowledges that we should not place full conviction on a specific value for the mean expected return. Instead, we allow for other potential return pathways where the mean expected return is different. Observing market data over the last 20 years only gives us information on one state of the world, or one regime. We cannot base our expected returns only on historic observation as future regimes can differ from the past, resulting in structural changes to the mean return. Second, our uncertainty varies by asset class. Why is this important? A lower ability to estimate returns for one asset class (for example when an asset’s returns are poorly explained by well-known public market factors) should be reflected with a wider uncertainty range, all else equal. For two assets of the same mean risk and return, we would hold less of the asset where we have greater uncertainty in the mean return assuming investors are averse to uncertainty. See the Banding together chart above.

Return Pathways

An assumption still commonly held in traditional portfolio construction techniques is that simulated asset returns (on an annualised cumulative basis) converge to a single point —the mean return —in the long-run. Our belief that there is mean return uncertainty leads to a different conclusion. The chart Questioning convergence compares two return simulations for US equities —one where there is no mean return uncertainty (the left chart) and one where we assume mean return uncertainty (the right chart).

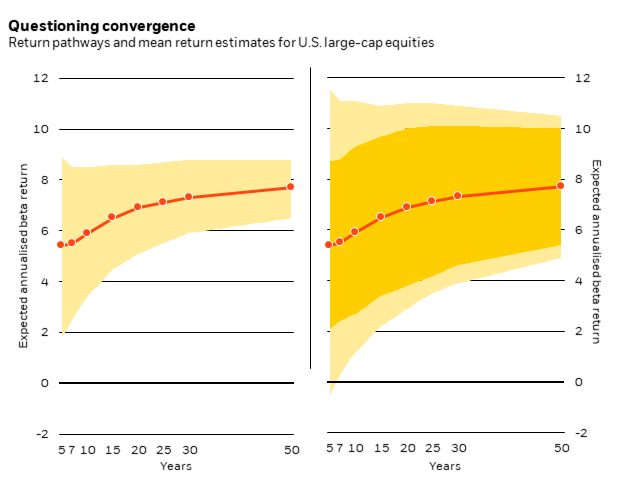
This information is not intended as a recommendation to invest in any particular asset class or strategy or as a promise – or even an estimate - of future performance. Source: BlackRock Investment Institute, April 2019. Data as of 28 February 2019. Notes: The line shows our mean (central) return estimate for large-cap US equities (MSCI USA) on a five-year to long-term horizon. Assumptions are total return and in US dollars. The interquartile range in light yellow shows the potential return pathways between the 25th and 75th percentiles generated by our stochastic simulation. The chart on the left shows this range based on the historical volatility of the asset class alone. The chart on the right includes the mean return uncertainty in orange. We discuss the factors determining the size of the mean return uncertainty above. Indices are not intended to be indicative of any fund or strategy’s performance. It is not possible to invest directly in an index.

Simulated returns with no uncertainty

With no uncertainty in the mean return, we see only a smaller, light yellow range. The range reflects the inherent risk of asset returns, or the standard deviation. It falls through time before eventually converging to the mean return estimate, or 7.5%, in this example. This will be a familiar picture to many. Simulated returns may have a forward-looking estimate of mean returns but assume no uncertainty in that mean. Importantly, the range of outcomes (the light yellow) is often based only on historic volatility.

Simulated returns with uncertainty

With uncertainty added, we see both a dark and light-yellow region. The range of outcomes does not and should never vanish to zero in theory and we see that the dark yellow region is persistent. Why? Collapsing to zero would require that the long-term expected return is known exactly (7.5% in our example). Instead of converging to a single point, the range of outcomes converges to the dark yellow band of uncertainty around our mean estimate at a horizon beyond 50 years. Another important consequence of adding uncertainty? The range of potential return pathways is wider than the range excluding uncertainty. This is because we now allow for more than just a single possible path of mean expected returns.

From theory to practice

Incorporating uncertainty brings the portfolio construction process closer to real-world investing experience: reality can stray considerably from any central expectation and the central expectation can be wrong, so we do not want to place all our bets on getting this right. How much uncertainty should we consider in return estimates? There is no single answer but several criteria guided our decision. We highlight the following:

Uncertainty and return simulations: The range of potential return pathways widens when including mean return uncertainty as shown in the Questioning convergence chart. But the bands representing the mean return uncertainty should be narrower than this full range of pathways including the historical volatility of an asset. This is intuitive: We would expect the range of daily stock prices to be larger than the range of the rolling average of those stock prices. This determines the relative scale of the shaded areas on the chart –the dark area should be narrower than the light.
Uncertainty and our cyclical views: We use asset class models, that capture the cyclical economic and market dynamics, to estimate returns at the five-year horizon. These views inform the five-year mean expected return in our simulations. At this horizon, the uncertainty band should be in line with the predictive power of our asset class models. In other words, we cannot have greater conviction in our five-year expected returns than is warranted by the back-testing of our asset class models.
Uncertainty and diversification: A portfolio construction framework incorporating uncertainty should deliver a solution that is between the MVO solution, that places full conviction on mean returns, and the minimum-variance solution, that places no conviction in mean returns. Too little uncertainty and an optimization will retrieve something close to mean-variance portfolio —typically very concentrated and requiring constraints. Too much uncertainty and an optimisation will retrieve something close to a minimum-variance solution that prioritizes diversification only. We are looking for a sensible middle ground.